Week 9: Classes 1

Week 9: Classes 1#

Important

First, download_week09.py and run the script in VSCode. You may need to confirm the download in your browser.

The script should end with Successfully completed!. If you encounter an error, follow the instructions in the error message. If needed, you can proceed with the exercises and seek assistance from a TA later.

Exercise 9: Introduction to classes

The goal of this week is for you to get accustomed to classes and, more generally with object-oriented programming. Object-oriented programming allows us to organize functions and data into logical units called objects.

An object can be thought of as a box that stores information that belongs together, simplifying data management from the programmer’s perspective. This approach is convenient, because it eliminates the need to store data in different variables, as all the data can be stored as attributes within one object. This approach is especially useful when dealing with large, complex programs that undergo frequent updates by multiple developers.

Let’s illustrate objects with an example: An object might represent a person, in which case it could have several attributes that describe a person, such as

first name
last name
nationality
etc.

This example touches on two essential features of object-oriented programming:

Objects tend to represent abstract entities or things. For instance, an object can represent a person.
In everyday language, there is a distinction between the concept of a person and the billions of instances of different people:

The concept of a person is characterised by having first and last name attributes, whereas a specific person, or an instance of a person, has a specific first and last name such as Donald and Duck respectively.

The concept of a person is called a class.
The specific instance of a person is called an object. There can be many such instances.

Here is an example of a class to define the concept of a person that can store their first and last names, followed by an example of how to create an instance of this class:

>>> class Person:
...     def __init__(self,first_name,last_name):
...         self.first_name = first_name
...         self.last_name = last_name
... 
>>> p1 = Person('Donald', 'Duck')

In order to define a class, the basic rules are as follows:

The definition of the class starts with class, followed by the name of the class, and a colon.
The class definition continues with the indented definition of the constructor __init__.
The arguments of the __init__ function, should be used to initialize all information that defines the state of the object.
The self variable is a reference to the object itself.

Here the __init__ function assign the arguments to attributes of the class e.g. self.first_name = first_name, as this is what’s required for initializing this class.

One can expand this class further to include a method which returns the full name of that person. The method is accessible from any instance of the Person class. That can be done as follows:

>>> class Person:
...     def __init__(self, first_name, last_name):
...         self.first_name = first_name
...         self.last_name = last_name
...     def get_full_name(self):
...         full_name= self.first_name+ ' ' + self.last_name
...         return full_name
... 
>>> p1 = Person('Donald', 'Duck')
>>> p1.get_full_name()
'Donald Duck'
>>> p1.first_name='Daisy'
>>> p1.get_full_name()
'Daisy Duck'

This example shows that class attributes are mutable. Even after having created p1 (which is an instance* of the Person class), we can change its attributes, just by accessing them and reassigning them (Donald changed to Daisy).

Summing up, the building blocks of object-oriented programming that one should prioritize familiarizing with are the following:

Classes: User-defined data types that act as blueprints for creating individual objects.
- In our example, the class used was Person.
Objects: Are instances of a class created with specifically defined data.
- In our example, the object was p1.
Attributes: Variables that live inside the instance of a class, that differentiate it from other instances of the same class.
- In our example, that were first_name, last_name.
Methods: Functions that are defined inside a class.
- In our example, we built the method get_full_name().

Note

Since object-oriented programming is about organizing, the simplest examples can seem trivial and useless. Keep this in mind for the first few examples where we try to introduce the syntax. Whenever feeling in doubt do not hesitate to consult chapters 15-17 in [Dow16], or look at the official Python documentation on classes here

Note

There are three main reasons why knowledge of object-oriented programming is valuable:

The main challenge for all programmers is writing code that is easy to understand and adapt to new demands. Object-oriented programming is the most popular way to accomplish this.
Everything in Python is, in fact, an object.
Widely used libraries, such as matplotlib, numpy, sympy and pytorch, use object-oriented programming extensively.

Exercise 9.1: Rectangle - Calculating Perimeter#

Exercise 9.1: Calculating Perimeter

As mentioned, objects tend to represent things, or concepts. In this exercise, you will create a class that represents a rectangle.

We start simple by including only a few attributes for the rectangle, later on, you are going to expand it by implementing additional attributes. To start, you are given a Rectangle class, which in order to be initialized, takes two arguments:

The width of the rectangle: width \(w\).
The height of the rectangle: height \(h\).

Rectangle also has a built-in method get_area(), which computes and returns the area of the rectangle:

>>> class Rectangle:
...     def __init__(self, width, height):
...         self.width = width
...         self.height = height
...     def get_area(self):
...         return self.width * self.height
... 
>>> rect = Rectangle(2, 3)
>>> rect.get_area()
6

As mentioned before, the method get_area belongs to this class and has access to all of the class attributes. Multiple methods can be defined within a class. When defining an additional method within a class remember the following:

The definition of a method should be indented with respect to the definition of the class, just like the __init__ method.
If the calculations within a method require information that is saved within the object, these are accessed through the self reference.
If any additional variables are needed to be passed to a method that are not contained within self, one can include them as arguments, separated by commas after self.

Your task is to implement an additional method (a function within the Rectangle class), similar to get_area, called get_perimeter. The function should calculate and return the perimeter of the rectangle. The perimeter can be calculated using the formula:

\[P = w + h + w + h = 2 (w + h)\]

The constructed method should work as follows:

>>> rect = Rectangle(2, 3)
>>> rect.get_perimeter()
10

To be able to test your method insert it in the file cp/ex09/rectangle.py.

class cp.ex09.rectangle.Rectangle(w, h, x_c=0, y_c=0)#

A class that represents a Rectangle.

get_perimeter()#

Compute the perimeter of a Rectangle-object.

Return type: float
Returns: The perimeter of the rectangle.

Exercise 9.2: Rectangle - Retrieving Corner Coordinates#

Exercise 9.2: Retrieving Corner Coordinates

Now, your task is to add additional attributes to the Rectangle class: x_c and y_c, representing the coordinates of the center of the rectangle. That means you need to update the __init__ function to store those attributes within self. After this, you should create a new method that returns the coordinates of the corners of the rectangle. You can always assume that the rectangle sides of length w and h are aligned parallel to the \(x\) and \(y\) axes, respectively.

You should return the corner coordinates as two lists of \(x\) and \(y\) values, starting from the lower left corner and moving clockwise.

>>> rect = Rectangle(2, 3, 2, 3)
>>> rect.get_corners()
([1.0, 1.0, 3.0, 3.0], [1.5, 4.5, 4.5, 1.5])

To be able to test your class and method insert it in the file cp/ex09/rectangle.py.

class cp.ex09.rectangle.Rectangle(w, h, x_c=0, y_c=0)

A class that represents a Rectangle.

__init__(w, h, x_c=0, y_c=0)

Construct a new Rectangle-object.

Parameters

w – The width
h – The height
x_c – The x coordinate of the center
y_c – The y coordinate of the center

get_corners()

Compute the corner coordinates of a Rectangle-object.

Return type: (list, list)
Returns: The lists of X and Y coordinates of the corner coordinates.

Exercise 9.3: Rectangle - Plotting Rectangles#

Exercise 9.3: Plotting Rectangles

It’s a good idea to consider visualization and well-formatted output to ensure you’re on the right track. One important takeaway from this example is that methods can accept additional arguments beyond those defined within a class.

Implement a method plot_rectangle, which plots the rectangle. In order to do so, the method can use the corner coordinates from the previous exercise. To illustrate that it is possible for a method to take additional arguments than what is defined within the class, you should also include an argument color to the method, which is the color of the plotted rectangle.

You can start by trying

plt.plot([0, 1, 0], [0, 1, 2], color='green')

What happens? How can you use this to plot the rectangle using the function from the previous exercise?

Using the method should look like this:

>>> rect = Rectangle(2, 3, 2, 3)
>>> color='red'
>>> rect.plot_rectangle(color)

(Source code, png, hires.png, pdf)

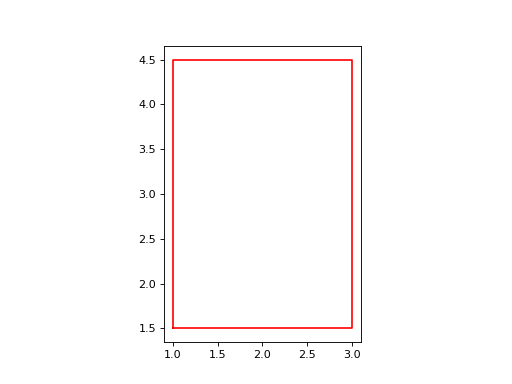
The purpose of this exercise is to illustrate that methods can also accept arguments and demonstrate how it’s done in practice. Here the argument color is not stored within the class as an attribute but rather outside of the class.

Note

This exercise has no tests associated with it and you do not have to exactly recreate the above plot, but are encouraged to experiment with how to best visualize the rectangle.

class cp.ex09.rectangle.Rectangle(w, h, x_c=0, y_c=0)

A class that represents a Rectangle.

plot_rectangle(color)

Compute the corner coordinates of a Rectangle-object.

Parameters: color – The color of the plotted rectangle.

Exercise 9.4: Vector - Introduction#

Exercise 9.4: Vector - Introduction

The focus of this last set of exercises will be a geometric (2D) vector.

We will represent a 2D vector, as \(\textbf{v} = (x,y)\).

Your first task is to implement the Vector class, which should describes 2D vectors, given their two coordinates. A vector \(v\) should have two fields, \(x\) and \(y\), corresponding to its two components along the \(x\) and \(y\) axis. The following should work:

>>> v = Vector(2, -3) # A vector v = (2, -3)
>>> v.x
2
>>> v.y
-3
>>> type(v)
<class 'cp.ex09.vector.Vector'>

To be able to test your class insert it in the file cp/ex09/vector.py.

class cp.ex09.vector.Vector(x, y)#

A class that represents a Vector, defined by the endpoint \((x,y)\).

__init__(x, y)#

Construct a new Vector-object.

Parameters

x – The x-component of the vector
y – The y-component of the vector

Exercise 9.5: Vector - Scaling#

Exercise 9.5: Vector - Scaling

In the rectangle exercises, we have already seen methods defined within a class. Let’s implement a method scale() for scaling a vector by a number \(s\). The method should exist within the Vector class, and it should take a single argument, \(s\), which is the scaling factor. The method should return a new Vector object, which is the scaled vector, and not modify the original vector.

Hint

In order to not modify the original vector the method needs to return a new vector, which is the scaled vector. The new vector can be created by using the Vector class constructor.

>>> v = Vector(2, 3)
>>> v_scaled = v.scale(1.5)
>>> (v_scaled.x, v_scaled.y)
(3.0, 4.5)

To be able to test your class insert it in the file cp/ex09/vector.py.

class cp.ex09.vector.Vector(x, y)

A class that represents a Vector, defined by the endpoint \((x,y)\).

scale(s)

Scale the vector self by a factor of s and return the scaled vector as a new Vector object.

Parameters: s (float) – A scalar number
Return type: Vector
Returns: The scaled vector.

Exercise 9.6: Vector - Addition#

Exercise 9.6: Vector - Addition

Now, we will work with a case that requires a method to take an instance of the Vector class as its argument, namely addition Implement a method add() which takes a Vector instance v as inputs, and returns a new vector with the sum of v and the instance self. \(u + w=(u_{x}+w_{x},u_{y}+w_{y})\).

Hint

Recall that since the input is Vector-objects, it will have fields such as v.x and v.y. Multiply these fields correctly and return the result: \(u \cdot w=u_{x} w_{x}+u_{y} w_{y}\).

When you are done, the following should work:

>>> v1 = Vector(1,2)
>>> v2 = Vector(3,4)
>>> v3 = v1.add(v2)
>>> (v3.x, v3.y)
(4, 6)
>>> type(v3)
<class 'cp.ex09.vector.Vector'>

To be able to test your class insert it in the file cp/ex09/vector.py.

class cp.ex09.vector.Vector(x, y)

A class that represents a Vector, defined by the endpoint \((x,y)\).

add(v)

Add the vector v to the vector self and return the sum as a new Vector object.

Parameters: v (Vector) – The vector to be added to self
Return type: Vector
Returns: The sum of the two vectors.

Note

The following exercises are part of Project 5: Working with classes. The link contains additional details, including how to hand in your results.

Exercise 9.7: Vector - Dot-product#

Implement a function dot() which accepts a vector v as input and returns their dot-product of \(v\) and the instance self, \(\mathbf{v}_1\cdot \mathbf{v}_2\) as a float.

When you are done, the following should work:

>>> v1 = Vector(2,1)
>>> v2 = Vector(2,3)
>>> v1.dot(v2)
7

To be able to test your class insert it in the file cp/ex09/vector.py.

class cp.ex09.vector.Vector(x, y)

A class that represents a Vector, defined by the endpoint \((x,y)\).

dot(v)

Compute the dot-product of self and v.

Parameters: v (Vector) – The vector to be dotted with self
Return type: float
Returns: The dot product of the two vectors.

Exercise 9.8: Translating Rectangles#

The objective of this exercise is to create an example that utilizes both of the classes Vector and Rectangle.

Implement a method of the Rectangle class, that takes a Vector as input translates the center of the Rectangle with the provided vector, such that

\[\begin{split}\begin{align*} \hat{x_c} &= x_c + v_x \\ \hat{y_c} &= y_c + v_y \end{align*}\end{split}\]

You can import the Vector class into the rectangle.py file with this line of code:

from cp.ex09.vector import Vector

The method should modify the existing Rectangle in-place, and thus not have a return statement. Using the function should look as follows:

>>> r = Rectangle(2, 2, 1, 1)
>>> (r.x_c, r.y_c)
(1, 1)
>>> r.translate(Vector(1, 1))
>>> (r.x_c, r.y_c)
(2, 2)

To be able to test your class insert it in the file cp/ex09/rectangle.py.

class cp.ex09.rectangle.Rectangle(w, h, x_c=0, y_c=0)

A class that represents a Rectangle.

translate(v)

Translate the rectangle by a vector v.

Parameters: v (Vector) – The vector to translate the rectangle by.

Week 9: Classes 1

Contents

Week 9: Classes 1#

Exercise 9.1: Rectangle - Calculating Perimeter#

Exercise 9.2: Rectangle - Retrieving Corner Coordinates#

Exercise 9.3: Rectangle - Plotting Rectangles#

Exercise 9.4: Vector - Introduction#

Exercise 9.5: Vector - Scaling#

Exercise 9.6: Vector - Addition#

Exercise 9.7: Vector - Dot-product#

Exercise 9.8: Translating Rectangles#